Taylor Dispersion Analysis explained
Taylor Dispersion Analysis is an ultra-low volume, microcapillary flow technique for sizing and stability of biomolecules in complex solutions, and offers advantages for orthogonal and complementary biophysical characterization measurements.
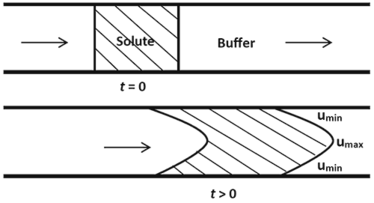
Taylor Dispersion Analysis (TDA) is a microcapillary flow-based technique whereby a nanoliter-scale sample pulse is injected into the laminar flow of run buffer, which then spreads out axially due to the combined actions of convection and radial diffusion. Detection of the equilibrium concentration profile (or Taylorgram) of the dispersed sample pulse allows the molecular diffusion coefficient and hence hydrodynamic radius of solute molecules to be calculated.
An instrument implementation utilising a UV area array detector in combination with two detection windows enables selective, mass-weighted sizing of small molecules, peptides and proteins, and samples with mixtures of these species. The TDA technique further lends itself to novel (label-free) analysis of the interactions, conformation and stability of proteins and other target molecules within complex biologically-relevant media e.g. excipient and/or surfactant-laden bioformulations, and aggregated solutions.
1. Introduction
Taylor Dispersion Analysis (TDA) is a fast and absolute method for determining the diffusion coefficients (and hence the hydrodynamic radii) of molecules. The method, sometimes referred to as Taylor-Aris dispersion, was first described by Taylor in his classic paper1, where he measured the dispersion of a pulse of solute injected into a flowing fluid in a capillary. In 1956, Aris developed the method further by accounting for the longitudinal diffusion of the molecules2.
Taylor’s deduction was based on his observation that the dispersion of the solute occurs via a combination of the radial diffusion of the molecules and convection due to the cross-sectional velocity of the fluid. A pressure-driven fluid in a cylindrical tube flows under Poiseuille laminar conditions3. This implies that the velocity of the fluid decreases radially from a maximum umax at the centre of the cylinder to a minimum umin at the walls of the cylinder. The effect of this velocity distribution on the profile of an injected solute pulse is illustrated in Figure 1.